Abstraction & Reasoning in AI systems : (3) deep learning with regard to abstraction
NeurIPS 에서의 < Abstraction & Reasoning in AI systems : Modern perspectives > 강연을 보고 그 중에서도 Francois Chollet 의 "why abstraction is the key, and what we're still missing" 에 대해 정리해보겠다.
(해당 강연은 https://slideslive.com/38935790/abstraction-reasoning-in-ai-systems-modern-perspectives 이 링크에서 확인할 수 있다.)
<3> what’s the role of deep learning in this picture what forms of abstraction deep learning can generate and where it fails
- capabilities & limits of deep learning with regard to abstraction
** Abstraction 관점에서의 Deep Learning
(1) value-centric abstraction 관점에서의 deep learning
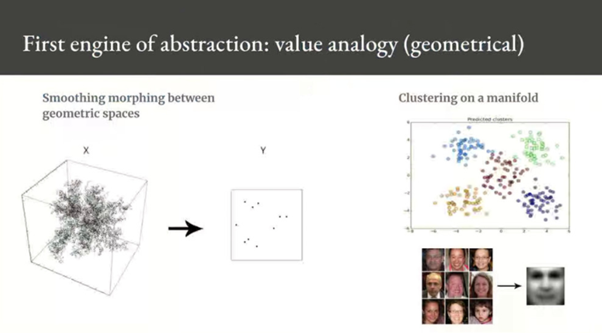
Deep learning excels at the first form of abstraction(value-centric) which makes sense because deep learning models are continuous, in fact, they are differentiable parametric model.
딥러닝은 첫번째 형태의 추상화(가치 중심)에서 우수하며 이는 딥러닝 모델이 연속적이기 때문에 맞는 말이다.
사실 딥러닝은 differentiable parametric (미분가능한 매개변수의) model 이기 때문이다.
따라서 딥러닝을 통해 기하학에 기반을 둔 abstraction 을 만들 수 있다는 것은 (맞는 말이고)직관적이다.
Supervised deep learning 에서 우리는 두 공간을 비교하게 되는데, 보통 인풋 벡터 스페이스가 있고 더 작은 타겟 벡터 스페이스가 있다. 이 두 공간 사이의 자연스러운 매끄러운 변화를 점 단위로 학습하는게 supervised deep learning 이다.
따라서 이것은 두 공간의 geometric analogy 이다.
더 확실하게 말하자면, 딥러닝 모델이 인코딩하는 것은 공간 대 공간 analogy 이다. 따라서 딥러닝은 learned distance function(학습된 거리 함수)를 통해 샘플들을 서로 연관시키는 것이며, 이는 매니폴드를 암시적으로 정의한다.
(2) program-centric abstraction 관점에서의 deep learning
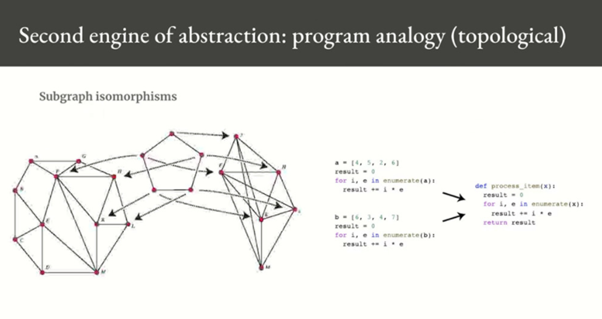
이제 두번째 abstraction 을 살펴보자. 이것은 앞의 geometric analogy 가 아닌 topology analogy 이고,
그래프들의 구조를 비교하고 subgraph의 isomorphism 을 찾아 추상화하는 것이 전부이다.
위 그림의 오른쪽 예시만 봐도 왼쪽의 두 프로그램은 a와 b 값 빼고 똑같은 구조를 가지고 있다.
이는 subgraph 의 isomorphism 이고, 따라서 detail 들을 제외하고 이를 process_item 이라는 것으로 abstraction 만들 수 있다.
** 보간 : 딥러닝의 일반화 시초

Value-based abstraction 으로 돌아가보자면, 이것은 머신러닝의 ‘manifold hypothesis’ 와 관련이 있다.
매니폴드 가설은 모든 natural 데이터가 데이터가 인코딩되는 고차원 공간 내의 저차원 매니폴드에 있다고 가정한다.
그리고 우리가 아는 한 이 가정은 거의 모든 perception problem 에 대해 정확하다.
MNIST 숫자, 사람 얼굴, 사람 목소리, 그리고 자연어까지에 대해서도 다 맞는 가정이다.
매니폴드 가설은 이러한 매니폴드들 중 하나 내에서 항상 두 input 간에 보간이 가능하다는 것을 의미한다.
즉 모든 점이 다 그 매니폴드에 떨어지는 연속 경로를 통해 한 입력을 다른 입력으로 변형하는 것이다.
데이터가 매니폴드에 위치한다는 것은 기본적으로 이러한 의미(한 입력을 다른 입력으로 변형 가능. 보간 가능)를 갖는다.
(보간 : 데이터들로부터 주어진 데이터를 만족하는 근사함수를 구하고 그 식을 이용해 주어진 변수에 대한 함수 값을 구하는 과정. 새로운 점을 만들기 위해 수 많은 점들을 평균화시키는 것. 두 점을 연결하는 방법을 의미.)
- 딥러닝 모델 : 매니폴드 얽힌 것을 풀기 위한 수학적인 도구
그리고 샘플들 사이에서 보간하는 능력은 딥러닝의 generalization 을 이해하기 위해 매우 중요하다.
이것은 딥러닝이 작동하는 이유(=보간)이다.
- 따라서 보간할 수 있는 데이터 점들이 있다면, 한 매니폴드에 있는 다른 점과 연관시켜 이전에 보지 못했던 점을 이해할 수 있다.
하나의 공간 샘플을 사용해서 공간의 전체성을 이해할 수 있는 것이 바로 generalization 이다.

딥러닝 모델은 기본적으로 매우 높은 차원의 곡선으로 model architecture priors 에서 비롯되는 구조상의 제약 조건이 있다.
그리고 이 곡선을 gradient descent 를 통해 fit 한다. 이 곡선은 모든 것에 fit 할 수 있는 충분한 parameters 들을 가지고 있다.
실제로 모델을 충분히 오랜 시간동안 훈련시키면 사실상 트레이닝 데이터를 다 암기하는 것으로 끝난다. 이건 전혀 generalization 되지 않은 것이다.
하지만 우리가 fitting 하려는 데이터는 input space 내에 고도로 구조화된 저차원 매니폴드를 형성하고 또한 gradient descent 가 진행되면서 시간이 지남에 따라 점진적으로 부드럽게 fitting 이 이루어지기 때문에 이 fitting 은 gradient descent 의 결과라고 볼 수 있다.
(위의 그림을 봐도 첫번째 트레이닝 전 모델 curve 는 랜덤에서 시작하고, 트레이닝할수록 better fit 으로 바뀌어가고 중간에 적당한 fitting 을 찾고 더 training 되면 overfitting 하는 fitting 변화를 볼 수 있다. 이 fitting 은 저차원 매니폴드 안에서 gradient descent 를 거치며 만들어진 부드러운 fitting 인 것)
훈련 중에는 모델이 과소적합과 과적합 사이에 있는 (=딱 적당한 좋은) 데이터의 natural manifold 와 대략 근사치를 갖는 전환점이 있다.
그리고 그 시점에서 모델에 의해 학습된 곡선은 실제 잠재된 데이터 매니폴드(the actual latent manifold of data) 를 따라 가깝게 이동하게 되고 따라서 그 모델은 보간을 통해 새로운 입력을 이해할 수 있게 될 것이다.
And an important observation here is that the power of this model to generalize is actually much more a consequence of the natural structure of the data rather than the consequence of any property of the model.
여기서 볼 수 있는 중요한 것은 generalize 하는 이 모델의 power 는 사실 모델 자체의 어떤 성질의 결과라기보다는 데이터의 natural structure 의 결과라는 점이다. (왜냐면 실제로 훈련을 통해 fitting 이 적절히 잘 된 curve를 보면 모델 자체의 특성을 보여주기보다는 원래 데이터 구조를 잘 나누는 잘 나타내는 그 자연 구조이기 때문에. 그리고 그 fitting 과정도 데이터 구조에 맞게끔 계속 변화되고 있었고..)
데이터가 점들이 보간될 수 있는 매니폴드를 형성해야만이 generalize 가능하고, 정보가 많고 노이즈가 적은 특징을 가질수록 generalization 하기 좋다. Input space 가 더 간단해지고 더 구조화되기 때문이다.
** Interpolative generalization 의 limitations

왜 deep convolutional networks 는 작은 이미지 변형에도 일반화를 잘 못할까?
- geometry based 의 interpolative generalization 은 작은 변화에도 민감하기 때문에
Interpolative generalization 은 인식 문제에 매우 효과적이지만 한계가 있다.
바로 깨지기 쉽고 작은 변화에도 민감하다는 점이다. 두 spaces 사이의 point by point mapping 이기 때문이다.
그리고 그 공간들 중 하나를 약간 이동시키면 학습된 매핑이 부서지게 된다.
( interpolative generalization 은 참고로 geometry based abstraction )
여기서 topology based abstraction 이 geometry based abstraction보다 더 강력하다는 것을 알 수 있는데,
거리(geometry based)는 작은 변화에 강하지 않기 때문이다. 그러나 구조(topology based)는 작은 변화에 강하다.
더 큰 한계점은,
Geometry based abstraction 이 관련성이 있으려면 continuous domain 을 처리해야하는데, 리스트를 정렬하거나 소수를 찾는 것과 같은 discrete 한 문제에 딥러닝을 적용할 수는 없다. 그리고 99퍼센트의 소프트웨어 엔지니어링 문제에 딥러닝을 적용할 수 없다.
이러한 문제들은 근본적으로 discrete 한 구조를 가지고 있기 때문에 continuous optimization 으로 해결할 수 없다.
따라서 이 이산형 구조를 연속형 매니폴드에 embedding 시켜볼 수는 있지만 보간에는 이 연속형 매니폴드를 사용할 수 없다.
따라서 연속형 parametric model 은 이전에 보지 못했던 것들에 대해 generalize 하지 못한다. 따라서 유용한 임베딩을 배우기 위해서는 그 문제 공간(the problem space)의 엄청난 샘플링이 필요할 것이고, 그 문제 공간 자체나 적어도 그 문제공간의 생성 문법은 외워야 할것이다. (아주 힘든 과정ㅜㅜ)
** 딥러닝을 적용시키기 위해 필요한 두가지

여기서 중요한 것은 주어진 문제에 대해 딥러닝을 적용시키려면 아래와 같은 두가지가 필요하다는 것이다.
1) “data points fit on a manifold where interpolation is meaningful(manifold hypothesis applies)”
데이터 점이 보간이 의미가 있는, 즉 매니폴드 가설이 적용되는 매니폴드에 fit 해야한다.
먼저 문제가 본질적으로 보간성이어야 하면서 보간이 의미가 있는, 즉 매니폴드 가설이 적용될 수 있어야 한다.
2) “there is a dense sampling of this manifold available(lots of training data)
매니폴드의 엄청난 샘플링이 가능해야한다. 즉 많은 트레이닝 데이터가 있어야 한다.
매니폴드를 학습하기 위한 충분한 데이터가 필요하고 보통 항상 엄청난 양이 필요하다. 따라서 학습하고자 하는 분포의 dense 한 sampling 이 필요하다.
- ARC 에 대해 흥미로운 것은 많은 사람들이 ARC 에 딥러닝을 사용하려고 해보았지만 아무도 성공하지 못했다. Single sample 도 해결하지 못했다. 그리고 이것은 GPT-3처럼 엄청 큰 pretrained models 에도 해당된다. ARC 문제들은 본질적으로 보간적이지 않으며 각 작업에 대해 몇 가지 예시만 있기 때문에 딥러닝으로 해결되지 못했다. (딥러닝 위 두가지 모두 해당 하지 않기 때문)
** 딥러닝은 value-centric abstracion 문제만을 해결할 수 있을 것이다.

Geoff Hinton 은 MIT tech review 에서 딥러닝은 모든 것을 할 수 있을 것이라고 말했다. 하지만 이것은 다 맞지는 않다.
딥러닝은 value-centric abstraction 문제만을 해결할 수 있을 것이다.
Program-centric abstraction 문제는 해결하지 못할 것이다.
인간이 인지와 직관을 통해 해결할 수 있는 모든 것은 아마도 충분히 큰 데이터셋을 얻을 수 있다고 가정할 때 딥러닝으로 해결할 수 있을 것이다. Reasoning, planning, program-centric abstraction 이 필요한 것은 모두 사실 딥러닝으로는 해결할 수 없다. 딥러닝으로는 해결이라기보다는 단순히 모든 암기일 뿐일 것이다.
다음 글에서는 딥러닝이 할 수 없는 abstraction 의 형태인 program-centric abstraction 을 generate 하기 위한 방법인 "discrete program search" 에 대해 다뤄보겠다.
(출처 : 해당 글의 이미지들은 NeurIPS 의 < Abstraction & Reasoning in AI systems : Modern perspectives > 강연 발표자료에서 가져왔다. )