트랜스포머(Transformer) (3) - 구조, 동작원리, 포지셔널 인코딩(Positional Encoding), 어텐션(Attention)

Deep Learning

트랜스포머(Transformer) (3) - 구조, 동작원리, 포지셔널 인코딩(Positional Encoding), 어텐션(Attention)

햇농nongnong 2022. 6. 4. 13:48

트랜스포머의 구조 - Attention Is All You Need

트랜스포머는 어텐션 기법만 쓰기 때문에 RNN, CNN 은 전혀 사용하지 않음
- 그래도 기존의 seq2seq 의 인코더-디코더 구조는 유지
- 인코더에서 입력 시퀀스를 입력받고, 디코더에서 출력 시퀀스를 출력
그렇기 때문에 문장 안에 포함된 각각의 단어들의 순서에 대한 정보를 주기 어려움
문장내 각각 단어의 순서에 대한 정보를 알려주기 위해 positional encoding 사용
이러한 아키텍쳐는 BERT 와 같은 향상된 네트워크에서도 채택됨
어텐션 과정 한번만 사용하는 것이 아니라 여러 레이어를 거쳐서 반복하도록 만듦
인코더와 디코더 N 번 만큼 중첩되어 사용하도록 만듦.
- 이전 seq2seq 구조에서는 인코더 / 디코더 하나에서 각 RNN 이 t개의 시점을 가지는 구조.
- 트랜스포머 논문에서는 인코더, 디코더 개수 6개씩 사용

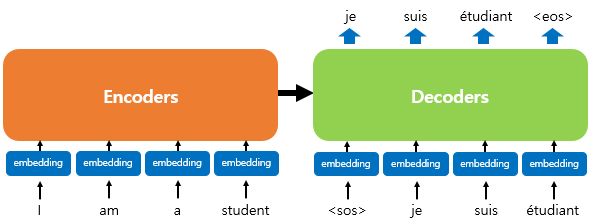
* 트랜스포머의 동작원리

입력 값 임베딩 (embedding)

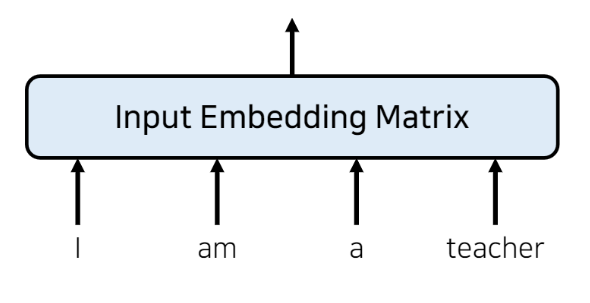
어떤 단어 정보를 네트워크에 넣기 위해서는 일반적으로 '임베딩' 과정을 거침
맨 처음에 들어가는 입력 차원 자체는 단어의 개수와 같기 때문.
이는 차원이 많을 뿐만 아니라 각각의 정보들은 원 핫 인코딩 형태로 표현되기 때문에 '임베딩' 과정을 거쳐 더욱 더 작은 차원으로 표현 - continuous 한 값 (실수 값) 으로 표현
ex) I am a teacher 문장이 들어오면 이를 input embedding matrix 로 만들기
이 입력 임베딩 행렬은 단어의 개수만큼 행의 크기를 가짐 (즉, 여기선 4개의 행)
각각의 열 데이터는 임베딩 차원과 같은 크기의 데이터가 담긴 배열 사용
임베딩 크기 (dimension)은 모델 아키텍쳐 만드는 사람이 임의로 설정 (이 트랜스포머 논문에서는 512 값 사용)
전통적인 임베딩 - 네트워크에 단어 정보 넣기 전, 입력 값들을 임베딩 형태로 표현
seq2seq 와 같은 RNN 기반 아키텍쳐를 사용한다고 하면, RNN 을 사용하는 것만으로도 각각의 단어가 RNN 에 들어갈 때 순서에 맞게 들어가기 때문에 자동으로 각각의 hidden state 값은 순서에 대한 정보를 갖게 됨.
- RNN 이 자연어 처리에서 유용했던 이유도 단어의 위치에 따라 단어를 순차적으로 입력받아서 처리하기 때문에, 각 단어의 위치 정보를 가질 수 있었기 때문이었음.

포지셔널 인코딩 (positional encoding)

트랜스포머와 같이 RNN 사용하지 않아서 단어 입력을 순차적으로 받는 방식이 아니라면, 문장 안의 각 단어들에 대해 어떤 단어가 앞에 오고 어떤 단어가 뒤에 오는지에 대한 정보를 따로 제공해야 함 = 위치 임베딩
따라서 트랜스포머는 'positional encoding' 을 통해 단어의 위치 정보(위치 임베딩)를 인코딩
- 단어의 위치 정보를 얻기 위해 각 단어의 임베딩 벡터에 위치 정보들을 더함

Input Embedding Matrix 와 같은 크기(dimension)를 가지는 별도의 (위치 정보를 가지고 있는) 인코딩 정보를 넣어서 각각 element wise 로 더해줌 (크기가 같기 때문에 element wise 더하기 가능)
별도의 위치 정보를 가지고 있는 포지셔널 인코딩 값을 구하기 위해 아래 두 개의 함수 사용

위의 함수인 사인 함수, 코사인 함수는 요동치는 모양을 하고 있는데, 트랜스포머는 이 사인 함수와 코사인 함수의 값을 임베딩 벡터에 더해주어 단어의 순서 정보를 더해줄 수 있음
- pos : 입력 문장에서의 임베딩 벡터의 위치
- i : 임베딩 벡터의 차원 인덱스
- d_model : 트랜스포머 모든 층의 출력 차원 (논문에서는 512)
즉 임베딩 벡터 내의 각 차원의 인덱스가 짝수인 경우에는 사인 함수의 값 사용, 홀수인 경우에는 코사인 함수의 값 사용함
- (pos, 2i) = 사인 함수, (pos, 2i+1) = 코사인 함수
따라서 포지셔널 인코딩을 사용하면, 각각의 단어가 어떤 순서를 가지고 있는지에 대한 정보를 네트워크가 알 수 있음
- 포지셔널 인코딩을 하면, 순서 정보가 보존됨
- ex) 각 임베딩 벡터에 포지셔널 인코딩 값을 더하면 같은 단어라고 하더라도 문장 내의 위치에 따라서 트랜스포머 입력으로 들어가는 임베딩 벡터의 값이 달라짐
즉, 트랜스포머의 입력은 순서 정보가 고려된 임베딩 벡터로 바뀌는 것임.
이 덧셈이 끝난 실제 입력 값, 즉 attention 이 받는 실제 입력 값 = 입력 문장에 대한 정보 + 실제 위치 정보

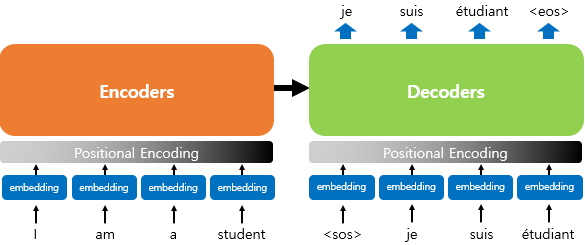
임베딩이 끝난 이후, 이 위치에 대한 정보까지 포함하고 있는 입력 값을 이제 attention 에 넣어줌

Positional Encoding

class PositionalEncoding(tf.keras.layers.Layer):
  def __init__(self, position, d_model):
    super(PositionalEncoding, self).__init__()
    self.pos_encoding = self.positional_encoding(position, d_model)

  def get_angles(self, position, i, d_model):
    angles = 1 / tf.pow(10000, (2 * (i // 2)) / tf.cast(d_model, tf.float32))
    return position * angles

  def positional_encoding(self, position, d_model):
    angle_rads = self.get_angles(
        position=tf.range(position, dtype=tf.float32)[:, tf.newaxis],
        i=tf.range(d_model, dtype=tf.float32)[tf.newaxis, :],
        d_model=d_model)

    # 배열의 짝수 인덱스(2i)에는 사인 함수 적용
    sines = tf.math.sin(angle_rads[:, 0::2])

    # 배열의 홀수 인덱스(2i+1)에는 코사인 함수 적용
    cosines = tf.math.cos(angle_rads[:, 1::2])

    angle_rads = np.zeros(angle_rads.shape)
    angle_rads[:, 0::2] = sines
    angle_rads[:, 1::2] = cosines
    pos_encoding = tf.constant(angle_rads)
    pos_encoding = pos_encoding[tf.newaxis, ...]

    print(pos_encoding.shape)
    return tf.cast(pos_encoding, tf.float32)

  def call(self, inputs):
    return inputs + self.pos_encoding[:, :tf.shape(inputs)[1], :]

어텐션 (Attention)

트랜스포머에는 세 가지 어텐션이 사용됨

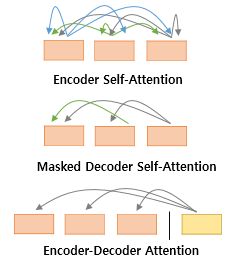
1) Encoder Self-Attention

인코더에서 이루어짐
self-attention : query, key, value 가 같음 (벡터의 값이 같은 것이 아니라, 벡터의 출처가 같음)
인코더의 self-attention : Query = Key = Value

2) Masked Decoder Self-Attention

디코더에서 이루어짐
디코더의 masked self-attention : Query = Key = Value

3) Encoder-Decoder Attention

디코더에서 이루어짐
디코더의 encoder-decoder attention
- Query : 디코더 벡터
- Key = Value : 인코더 벡터

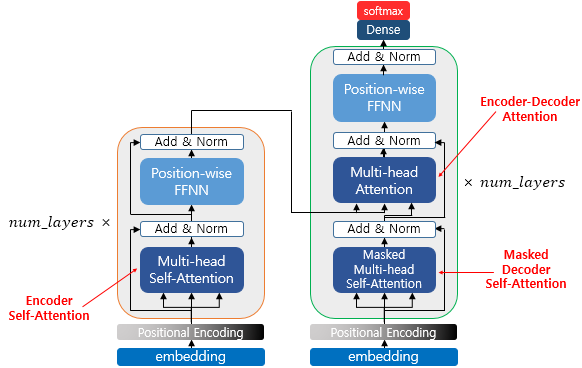
위의 세 가지 어텐션은 트랜스포머 안에서 위의 그림과 같이 위치해있음.
세 가지 어텐션에 추가적으로 "multi-head" 가 붙어있는데, 이는 트랜스포머가 어텐션을 병렬적으로 수행하는 방법을 의미함.

셀프 어텐션 (self-attention)

트랜스포머에는 셀프 어텐션이라는 어텐션 기법이 등장
셀프 어텐션 전에, 먼저 어텐션을 살펴보자.

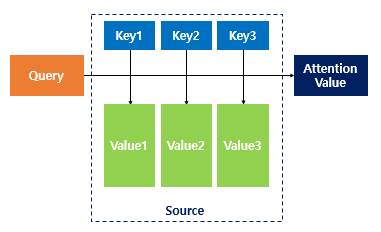
앞의 seq2seq with attention 에서 에너지값 - 어텐션 스코어를 구할 때 행렬곱을 통해 유사도를 구했던 것처럼, 어텐션 함수는 유사도를 구하는 함수
주어진 쿼리(Query)에 대해서 모든 키(Key)와의 유사도를 각각 구하고, 이를 가중치로 하여 키와 매핑되어 있는 각각의 값(Value)에 반영
그리고 유사도가 반영된 값(Value) (= Value1, 2, 3)을 모두 가중합하여 최종 리턴 = Attention Value

그렇다면 셀프 어텐션이란?

어텐션을 자기 자신에게 수행한다는 의미

먼저, Query, Key, Value 에 대해 자세히 알아보자.

앞 포스팅에서 봤던 seq2seq with attention 의 경우, Query, Key, Value 는 아래와 같다.

2022.06.03 - [Deep Learning] - 트랜스포머(Transformer) (2) - Attention 으로 seq2seq 문제 해결

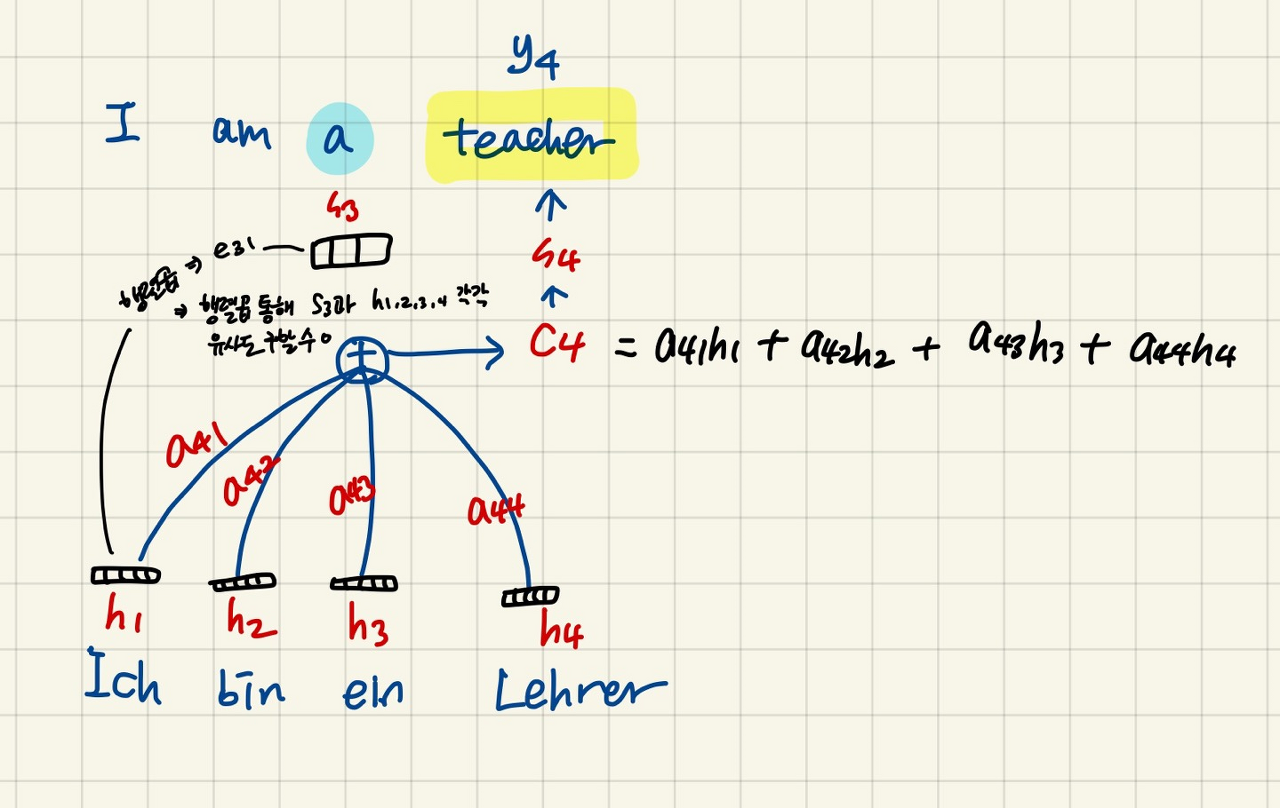
디코더 셀에서의 은닉 상태였던 s3 를 각각의 h1, h2, h3, h4 와 곱해주는 형식이기 때문에, s3가 Query, h1, h2, h3, h4 가 Key 라고 할 수 있다. 그리고 각각 행렬곱의 결과들이 Value 이고, 이를 다 더해서 c4 가 만들어지게 된다.
Q = Query : t 시점의 디코더 셀에서의 은닉 상태
K = Keys : 모든 시점의 인코더 셀의 은닉 상태들
V = Values : 모든 시점의 인코더 셀의 은닉 상태들

시점은 계속 변화하면서 반복적으로 쿼리가 수행되기 때문에, 시점 t 를 전체 시점으로 일반화 할 수 있다.

Q = Querys : 모든 시점의 디코더 셀에서의 은닉 상태들
K = Keys : 모든 시점의 인코더 셀의 은닉 상태들
V = Values : 모든 시점의 인코더 셀의 은닉 상태들

이처럼 위의 예시에서는 디코더 셀에서 Query 가 있었고, 인코더 셀에서 Key 가 있었기 때문에, Q 와 K 가 서로 다른 출처, 즉 서로 다른 값을 가지고 있다.

하지만, 셀프 어텐션에서는 Q, K, V 가 전부 동일
트랜스포머의 셀프 어텐션에서의 Q, K, V 는 아래와 같음
Q : 입력 문장의 모든 단어 벡터들
K : 입력 문장의 모든 단어 벡터들
V : 입력 문장의 모든 단어 벡터들

그렇다면 셀프 어텐션의 효과는?

위 그림에서 "그 동물은 길을 건너지 않았다. 왜냐하면 그것은 너무 피곤하였기 때문이다." 라는 문장
여기서 그것(it)은 당연히 동물(animal)
우리는 피곤한 주체가 동물이라는 것을 쉽게 알 수 있지만, 기계는 이 it 가 길(street)인지 동물(animal)인지 쉽게 알기 어려움.
따라서 셀프 어텐션을 통해 입력 문장 내의 단어들끼리 유사도를 구해서 it 이 animal 과 연관되었을 확률이 높다는 것을 찾을 수 있음.

트랜스포머에서의 셀프 어텐션 동작 메커니즘

셀프 어텐션은 위의 예시들처럼, 단어들 사이의 유사도를 구할 때 주로 이용하고, 따라서 입력 문장의 단어 벡터들을 가지고 계산한다.

트랜스포머에서의 셀프 어텐션 동작 메커니즘을 이해하기 위해 먼저 인풋을 생각해보자.

위에서 설명했던 포지셔널 인코딩을 거치면 위치 정보가 포함된 최종 input embedding matrix 가 만들어졌음.
d_model 차원의 초기 입력 input embedding matrix 단어 벡터들을 바로 사용하는 것이 아니라 각 단어 벡터들로부터 먼저 Q, K, V 벡터들을 얻어야 함.

1) Q, K, V 벡터 얻기

이 Q, K, V 벡터들은 초기 입력의 d_model 차원의 단어 벡터들보다 더 작은 차원을 가짐.
- 트랜스포머 논문에서는 d_model = 512 의 차원을 가졌던 초기 단어 벡터들에서 64차원의 Q, K, V 벡터로 변환하여 사용
- d_model / (num_heads) = Q, K, V 벡터의 차원
- 트랜스포머 논문에서는 num_heads를 8로 하여 512 / 8 = 64 로 Q, K, V 벡터 차원 결정

ex) "I am a student." 에서 student 라는 단어 벡터를 Q, K, V 벡터로 변환

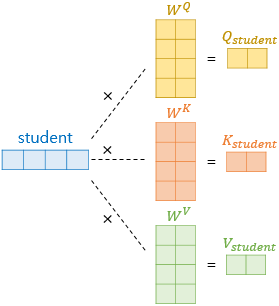
기존의 512 차원의 벡터로부터 더 작은 벡터 Q, K, V 를 만들기 위해서는 가중치 행렬을 곱해야함
가중치 행렬의 크기 : d_model * (d_model / num_heads)
- 논문의 경우에서는 512 * 64
- 그럼 (1 * 512) x (512 * 64) = (1 * 64) 로 더 작은 벡터인 Q, K, V 구할 수 있음.
- 이 때, Q, K, V 벡터를 만들기 위한 가중치 행렬은 각각 다름.
- 따라서 512 크기의 하나의 student 단어 벡터에서 서로 다른 3개의 가중치 행렬을 곱해서 64 크기의 서로 다른 3개의 Q, K, V 벡터를 얻음.
- 이 가중치 행렬은 훈련 과정에서 계속 학습됨.
"I am a student." 문장의 모든 단어 벡터에 위의 과정을 거치면, I, am, a, student 단어 각각에 대해서 서로 다른 Q, K, V 벡터 구할 수 있음.

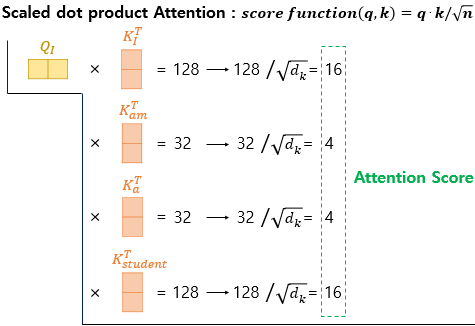
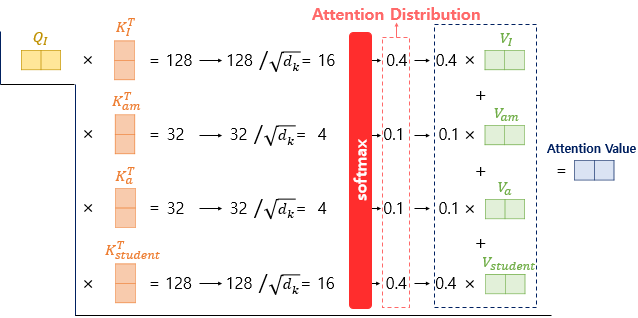
2) Scaled dot-product Attention 수행하기

현재까지 Q, K, V 벡터들을 얻은 상황. 이제 기존의 어텐션 메커니즘과 동일한 작업 수행
먼저 각 Q 벡터는 모든 K 벡터들에 대해서 어텐션 스코어 구함 - 어텐션 분포를 구함 - 어텐션 분포로부터 가중치를 적용해 모든 V 벡터들을 가중합함 - 최종 어텐션 값 ( = context vector) 구함
위의 과정을 모든 Q 벡터에 대해 반복
어텐션 스코어를 구하기 위한 어텐션 함수는 가장 기본인 내적 dot product 이외에도 종류가 다양함
트랜스포머 논문에서는 기본 내적에다가 특정 값으로 나누어주는 어텐션 함수를 사용

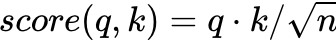
위의 함수처럼 특정 값으로 나누어주는 것을 기존의 내적 (dot-product attention) 에서 값을 스케일링했다고 표현하여, Scaled dot-product Attention 이라고 함.

Reference

이 글은 나동빈님의 'Transformer : Attention Is All You Need' 논문 리뷰 영상을 보고 정리한 글입니다.